Homework???

After spending a day immersed in an initial training at a recent Tabor Rotation Institute, participants placed several sticky notes on the “parking lot” of questions. I promised I’d blog about those questions.
“When do you give homework?”
“When do you check homework?”
“When you’re using math stations and guided readiness groups, how will you have enough time check homework?”
These are valid questions, especially when a teacher or school is beginning to use small-group, differentiated instruction in math using the Tabor Rotation Framework and homework is mandatory. This next question is the one most frequently asked.
“Do you believe in homework and how do you use it with your students?”
A discussion on the belief in homework could encapsulate quite a few hours of heated discussion and debate. I have studied the topic with an open mind and from varied perspectives. (I’ll share some links in this blog.) You can find studies that support many varied views, but most agree on one assertion,
“The quality of homework assignments is more important than the quantity of time students spend on them.” -Homework Expert, Harris Cooper of Duke University
Robert Marzano and Debra Pickering, in their article, “The Case For and Against Homework” assert that there is great value in the right kind of homework. They support schools making policies that ensure homework will produce learning gains. Here are their general guidelines.
-Assign purposeful homework.
-Assign homework that is likely to be completed.
-Involve parents in appropriate ways.
-Don’t overdo it.
-Follow up with students.
Linda Darling-Hammond and Olivia Ifill-Lynch provide additional insight into effective ways to get students to do their homework in, “If They’d Only Do Their Work.”
Here’s a summary of the key points of their article.
-Assign work that is worth of effort. Teachers should be examining homework assignments and asking questions. What is the purpose of this assignment? Do students have the support to complete it? Does it make sense? Is it necessary? Most important, is it authentic and engaging?
-Make the work doable. Teachers need to make sure that directions are clear and that the work can be done independently.
-Find out what students need. The goal is to make the process of doing the assignment transparent, concrete, manageable, and as simple as possible. The point is for the student to learn that it feels better to succeed than to fail.
-Create space and time for homework. Some schools have put in place systematic ways of ensuring that students have opportunities to get their schoolwork done in school. As founding principal of Manhattan East Middle School Jacqueline Ancess asserts, “The school needs to make it harder not to do the work than to do it!”
-Make work public. When schools engage students in major projects [or even in minor ones], it is important to show them models of work and exhibitions that meet the standards. This practice helps demystify the work, demonstrates that it can be done, and illustrates how to do it.
-Encourage collaboration. Schools that are organized as supportive learning communities with opportunities for collegial problem solving can better support their students in developing the practices and habits essential to doing schoolwork.
One homework criteria, from Cathy Vatterott’s article, “Five Steps to More Effective Homework,” really made me stop and think.
Decriminalize grading!
“Homework should not cause students to fail. Holding students accountable for homework should mean insisting that they finish rather than giving them a zero.”
The list below provides good guidelines for this.
-Have a zeros aren’t possible policy—all work must be completed.
-Use homework to check for understanding and give feedback.
-Don’t kill motivation or course grades by being too punitive.
-If possible, don’t give grades at all; give credit for completion only, not correctness or accuracy.
-Count homework for 10 percent or less of final grades.
-Be somewhat lenient on lateness; allow re-dos or give incomplete until the work is finished.
Vatterott’s work is worth reading and gives many more ideas for making sure homework is not only done, but contributes greatly to learning.
The research provided in this blog was put there to help you, your students, and the parents understand how to make homework as meaningful and purposeful as possible. But, you may still have the same concerns that some participants have at the end of a Tabor Rotation Institute Training.
Teachers who are trained how to transform their classroom using the Tabor Rotation Framework really don’t want me to share the research or quote the theorists. Most are required by their departments, schools, or districts. What most teachers want are some answers, they want to know how I incorporated homework into a classroom that is student-centered and focused on engagement instead of rote practice.
Below are suggestions that have proven to be highly successful with students who use Tabor Rotation and are accustomed to engaging and meaningful instruction. It’s what I did with my students.
*Make deadlines flexible. I assign a week or unit of homework/productive practice all at the same time with a final turn-in date. I give specific dates for certain homework items to be completed and brought into class so that students have practice with concepts that build on each other.By giving the homework assignments all together it allows those students who have varying commitments to complete the homework when their schedules allow.
*Give students time to complete homework/productive practice during the school day. I allow students to complete homework during daily warm-ups, during extra study periods, and during choice board selection or independent work. Some students do not have a home environment that is conducive to working on anything and may never finish any work or practice at home. Homework then becomes punitive. This was counter productive and I just didn’t do it! Homework was never more than 10% of their grade.
*Provide the teams with the answers. You don’t need to review all of the problems–just the most important ones. This allows students time to check their work and then move to the discussion of which ones were most challenging and which ones were the simplest. The discussion and the process of their learning was more important to me than having all the right answers.
*Make homework collaborative. If my students spent time working, then I wanted them to be able to share it with someone else besides me and receive feedback from their peers, too. Before checking homework, I have students work with their partner and share the most challenging problem and the simplest problem from their homework and why they found it challenging or simple. I encourage discussion on how they solved the most challenging problem or the steps they took in attempting to solve it. Students should be able to ask for assistance from their partner or another member of their team.
*Use homework results as part of Guided Readiness Group Instruction. I conduct progress monitoring using Passports, Clipboard Cruising, Exit Questions, and formative assessments. I use this information to form Readiness Groups during Phase 3 of Tabor Rotation, but homework results should also be used. You can also circulate and use teachable moments during Homework Check.
*Ensure homework is interesting and purposeful. I always make some portion of the homework assignment have a purpose beyond rote practice. I make sure that it is used for something outside of class. I also put a social component into the homework that encourages purposeful interaction with a family member or with a team member.
*Make sure the students can do the work independently. My rule of thumb was “if it takes you more than the amount of time we spent on it in class, then record your efforts and bring it in to discuss. Homework isn’t purposeful or productive when it becomes painful to my student and/or their parents.
As I think about my years of assigning homework, there is one consistent truth. No student has ever come back and thanked me for giving them homework. They come back to thank me for making school fun, meaningful, purposeful, and engaging. They thank me for all the cool things we did that didn’t even seem like work. They tell me they remember everything we did like it was yesterday.
I’m going to take that to mean the homework was pretty good, too!
What is the Rest of the Class Doing?
“There are two primary choices in life: to accept conditions as they exist or to accept the responsibility for changing them.” -Denis Waitley
The first challenge of differentiated Readiness Groups, based on your students’ level of understanding of skills and concepts, is realizing that all students deserve the opportunity to move further ahead in their depth of understanding. This is Phase Three of the Tabor Rotation Framework and typically occurs on Days 4 and 5 of a week of Tabor Rotation.
The second challenge, for most teachers, is figuring out meaningful, respectful, and qualitatively challenging ways of engaging the remainder of the students while the teacher is guiding the math readiness groups. Choice Boards are an excellent option.
What is a choice board? Essentially, a Choice Board is an outline of instructional options that are targeted toward important learning goals and are based on the state standards for the students’ grade level/subject. The teacher directs the process, but they are called “Choice” Boards because students are given some type of control or choice over their selections. This choice includes the items that most appeal to them and the order of completion.
Choice Boards typically have nine cells or spaces. This Choice Board Template is differentiated or tiered based upon the student’s level of understanding. I worked with a group of high school and junior high students to develop the names for the levels: Novice, Pro, Master. They felt these were descriptive but not demeaning.
This example of a Choice Board or Choice Menu was developed by a secondary level teacher. It includes options that must be completed by all students (a Check for Understanding and turned in for a grade), requires completion of the Passport to the Tabor Rotation Stations, and then selection of at least 5 assignments. The teacher also asked that the students select one choice from each column and that their choices equal at least 12 points.
This high school teacher, who strongly believed in small-group instruction at all levels, said her Algebra II Honor students loved this type of Choice Board and felt greatly empowered when they began to work independently. The Choice Menu also gave their teacher time to work with her Algebra II Honors students to move each level (approaching, at, above) ahead in the curriculum.
Tabor Teachers have also found the “Menu” Selection to be an exciting way to provide choices for their students. Chris Tienken, in a presentation to Keansburg, New Jersey Schools, shared some excellent examples. I like that students all have to do the “Main Dish” activities, select two of the “Side Dish” activities, and then may choose optional “Desserts” if they finish their other choices. Take a look at Chris’ slide show presentation to learn more about “Menus” and differentiated instruction in general.
What if you want to hold Guided Math Readiness Groups and are ready for Phase Three of Tabor Rotation, but creating a 9-Cell Choice Board is simply too much to think about right now. I like the adaptations suggested by Carol Ann Tomlinson in her book, Fulfilling the Promise of the Differentiated Classroom. I’ve also added a few of my own adaptations that have worked well with my larger, more diverse classes.
- Allow students to complete any 3 tasks in the order they choose.
- Assign students a few specific tasks based on readiness and tasks everyone completes.
- Base the Choice Board on students’ learning styles or learning preferences. This example with column headings was developed by a primary school based on varying modalities.
- For those students who are less independent, allow them to work with a partner and teach them how to scaffold support for one another without “doing the work” for each other.
- Assign the more complicated choices to a student who becomes the “Master of the Task.” Explain how to complete the assignment to that one student and write their name next to the task. If a student doesn’t know how to do it, they go to the “Master of the Task,” not you, for assistance.
- Provide answer keys so students can check their own work. I typically asked students to check their partner’s work, not their own.
- Create a Choice Board that will last for 2-3 weeks or an entire unit of study instead of just one week.
If you’re looking for more ideas for creating Choice Boards, key search words are Choice Menu, Learning Menus, Tic-Tac-Toes, Tic-Tac-Toe Menus, Custom Boards, Tiered Activities, and Extension Organizers. When you and your team are in the planning process for a unit or quarter of instruction, you will be able to find a plethora of examples. Some will be accurate and some will not, so be sure to read and to complete the choices (Yes, someone on your team needs to complete each of the activities before giving them to your students.)
Below are just a few of the websites that will help you in your journey to create meaningful and engaging independent activities. You will find many more websites or pins linked to all of these websites. Your dilemma may not be how to find a Choice Board, but which ones are best for your class’ needs.
https://daretodifferentiate.wikispaces.com/Choice+Boards
http://tobytheteacher.wikispaces.com/Choice+Boards
http://www.pinterest.com/tahamati/choice-board/
http://quality.cr.k12.ia.us/DI/DI_ChoiceBoards.html
“You can’t make positive choices for the rest of your life without an environment that makes those choices easy, natural, and enjoyable.” -Deepak Chopra
Final quote for those of you who are concerned about your first efforts in using Choice Boards with your class,
“As a child, my family’s menu consisted of two choices: take it or leave it.” -Buddy Hackett
Why Teach Guided Math?
“We always hope for the easy fix: the one simple change that will erase a problem in a stroke. But few things in life work this way. Instead, success requires making a hundred small steps go right – one after the other, no slipups, no goofs, everyone pitching in.” -Atul Gawande, Better: A Surgeon’s Notes on Performance

The antique in the picture above reminded me, once again, of the importance of teacher-guided, small-group instruction in math. I know, it’s probably tangential thinking like a 1st grader, but let me explain.
This buffet has been in my husband’s family for over a hundred years. It is made of solid wood in a mission style. It was built in the late 1880’s and has the most interesting and distinctive marks on it. One of the marks was made from an old-fashioned flat iron that was accidentally left on the surface. The triangular mark is a commentary on history, especially when most of my students have never even used an iron. (And, no, as I explained to an 8th grader the other day, there isn’t an app for that!)
The part of the buffet that has stood out to me for years isn’t it’s workmanship, the grain in the wood, or its history. It is the fact that one of the doors just would not stay closed. We tried propping up one side of the doors with a shim. This held the door in place for a while, but then someone would open the door, the shim would fall out, and the door would flop open again. We tried propping up one of the legs of the buffet. This just made the piece look odd. For over ten years, we have used twist ties, twine, rope, rubber bands, stretchy wrist bands, slap bands…just about anything that was conveniently nearby when the door popped open.
A few months ago, the buffet was moved to a different room and we decided to store other items in it. I was putting some things away in the cabinet space behind the doors last week and dropped a placemat on the floor. I looked at that buffet from a different angle and in a different light.

That’s when I noticed something on the top part of the “always open” door. Instead of finding a quick fix, I began to look at the door. There was something on the top edge I had never noticed before. It was a small piece of metal that had been covered over with dust and paint. Hmm!
After decades of banding the door shut I realized that we had never looked for the cause. We just assumed it was just old and not repairable. I got a flashlight and looked underneath the edge of the cabinet. Sure enough, under the edge of the cabinet was an indention where a magnet used to be. With a new magnet in place, the door closes and stays closed without any effort. I just needed to look closer at the cause instead of using the quickest and easiest fix.

The connection?
If teachers only use whole-group instruction, worksheets, and meaningless activities when teaching mathematical concepts, they may never find the cause of the challenges a student is facing.
Without small-group instruction, a teacher may never realize that a student has great computational skills, but has simply memorized one step in the algorithmic procedure incorrectly.
If a student is never given the opportunity to explain their thinking, then their brilliant spatial intelligence may never be cultivated by anyone.
My discovery helped me enjoy an antique instead of finding it irritating—what a small thing compared to what happens in a classroom. Taking the time to look under the surface, to actively listen to your students, to use engaging strategies, to give them a time to share their thinking with you and each other in a guided, small-group setting is invaluable. And, it will probably change your students’ lives forever.
“Unless someone like you cares a whole awful lot, nothing is going to get better. It’s not.” -Dr. Seuss
More about AHA Moments
An Aha Moment, according to the Merriam-Webster Dictionary, is a moment of sudden realization, inspiration, insight, recognition, or comprehension. But the question is,
Why would this be the content of a keynote speech I presented today at the South Carolina Council of Teachers of Mathematics (SCCTM) Annual State Conference?
It’s simple. SCCTM’s Annual Conference is filled with so many incredible sessions that explore a wide variety of topics. The most challenging part of the day is selecting the sessions to attend and knowing there are so many other really good sessions.
However, none of these sessions will bring full results unless the information shared during them impacts the lives of students. I believe this and it’s why I set aside time during every training session to share ways for teachers to cultivate a classroom atmosphere that encourages aha moments.
There are many good sources for learning more about aha moments. To keep this blog post from being way too long, I’ve included some key points and the links to the entire source. All of them are well worth the few minutes it takes to read them. Each of them would also be excellent read alouds for your whole class as you help them fine-tune their recognition and use of aha moments.
Maximizing Aha Moments
Bruce Dorminey’s article for Forbes.com, “Maximizing Those Aha Moments Still Key to Our Future,” describes what insight is and the difference between insight and intuition.
Intuition is use of patterns we’ve already learned while insights are the discovery of new patterns. With an insight you don’t necessarily have a feeling that there’s something there. It hits you without warning. It shifts the story that you’re telling yourself, whereas intuition uses the patterns that you already know or have. An insight suggests new patterns.
“Aha!” moments hit us all. Although they can range from new ways to tie a shoelace to ideas for the latest smart phone, acting upon such “insights” remains key to our collective future. Read all of Bruce Dorminey’s article.
Barbara Morris, President of LaserImage, shares how to maximize your aha moments in her article, “The Art of Leaning into Your Aha Moment.” Even though she is focusing on aha moments in a corporate setting, the ideas are definitely applicable in an education setting.
A lot of great ideas start as scrawled notes on bar napkins. And a lot of those same great ideas are tossed away and never become what they could. People are scared to take risks, they don’t have enough money to turn their idea into a reality, or they’re too busy to transform themselves from followers into innovators. Just because you face challenges, though, doesn’t mean you can’t turn a big idea into a bigger reality. Read all of Barbara Morris’ article.
The Science of Aha Moments
For those readers who are becoming skeptical at this point, there is scientific proof that aha moments exist. Aha moments can be seen inside the brain. WebMD.com describes a scientific study in which researchers found an increased activity in a small part of the right lobe of the brain when the participants reported creative insight during problem solving. Little activity was detected in this area during non-insight solutions. Web MD’s Scientists Explain the Science of Aha Moments
If you want to read more about scientific evidence for aha moments, the study by Kounios and Beeman is fascinating!
In a series of experiments, Kounios and Beeman found that volunteers who experienced insight experienced a distinctive spark of high gamma activity that would spike one-third of a second before volunteers consciously arrived at an answer. Additionally, the flash of gamma waves stemmed from the brain’s right hemisphere—an area involved in handling associations and assembling parts of a problem.
Gamma activity indicates a constellation of neurons binding together for the first time in the brain to create a new neural network pathway. This is the creation of a new idea. Immediately following that gamma spike, the new idea pops into our consciousness, which we identify as the Aha! Moment. More about Kounios & Beeman’s Aha Moment Experiments
Educators and Aha Moments
As an educator who believes in giving students time for information to absorb, Daniel Goleman’s post, “Maximize Your Aha Moment,” really hit home.
The pre-work for the gamma spike includes defining the problem, immersing yourself in it, and then letting it all go. It’s during the let-go period that the gamma spike is most likely to arise and along with that the “aha” or “light bulb over the head” moment. Read all of Daniel Goleman’s article on maximizing your aha moments.
“Reassessing the Aha Moment” by Janet Rae-Dupree really addresses the role that the classroom teacher plays in the facilitating of aha moments.
…as soon as you dig into what happened five minutes before that magic moment, or a day, or a week, or a month,” he said, “you realize that there is a much more complicated story in the background.” That more complicated story most often begins and ends with a determined, hard-working and open-minded person trying, and failing, to find a solution to a given problem.
It’s not that these magical moments of epiphany don’t happen. In small ways, they happen all the time. But they are not nearly as important as what the innovator did before – or ultimately does after – the magic light bulb goes on. “Reassessing the Aha Moment” by Janet Rae-Dupree
What if a teacher or professor just simply believes in a student and shares his or her enthusiasm with their students? It changed the life of Sharon Matola, known as the “Zoo Lady” to over 12,000 children who visit her and Belize’s only zoo for orphaned animals that she founded in 1983. She doesn’t remember all the details of her inspiration, but she does remember the power of belief in your students,
“My professor told me I was smart. He was the only professor who said that.”
Read Sharon Matola’s story and others who experienced aha moments in education.
The “How to” of Aha Moments
Dr. Marcia Reynolds, in “Creating the Aha Moment,” lists the following Brain Tips for creating aha moments.
Brain Tip 1. Do something else. Give your brain a chance to restructure itself, letting your right hemisphere access your long term memory to bring a new solution into view.
Brain Tip 2. Give it a rest. If you can, take a nap or put the problem away for a day to let your brain sleep on it. While you sleep, the hippo campus goes to work connecting data with knowledge in new ways.
Brain Tip 3. Have fun. While you are eating that ice cream cone or watching a funny movie, your middle brain is unconsciously looking at your problem from different angles.
Brain Tip 4. Work with your coach. An experienced coach is well trained to ask you the question or provide the metaphor that breaks through your frame of thinking. You literally look at the problem from a new angle.
Learn more about how to create aha moments.
Dr. Bruce Johnson describes the failures of schools to cultivate creativity. He discusses the theories of Jeffrey Selingo, editorial director of The Chronicle of Higher Education, who encourages teachers to break the traditional teaching practice of memorization and regurgitation. Instead, students should be completing projects that require creativity and application of the knowledge they’ve gained.
Dr. Johnson also lists some ways to tap into your inner creative self.
1. Know When to Work and When to Stop
When you feel the need for a break that’s an indication you either need an alternate perspective or additional information. And research shows you are likely to get the insight or “aha” moment once you step away from the project or problem.
2. Tap Into Your Imagination
You can synthesize experience; literally create it in your own imagination. The human brain cannot tell the difference between an ‘actual’ experience and an experience imagined vividly and in detail.” Walt Disney said “if you can dream it, you can do it.” That forms the basis for creativity, being able to dream and then put your imagination to work.
3. Develop a Mindset for Creativity
This is probably the one barrier that prevents students from learning to develop their creative capacity, a limiting self-belief. The statement, “I’m not a creative person” can limit your possibilities. You can train yourself to be creative simply by allowing time to use your imagination.
Train yourself to think more creatively.
Final Thoughts on Aha Moments
Oprah.com defines aha moments as…a moment of clarity, a defining moment where you gain real wisdom-wisdom you can use to change your life. Whether big or small, funny or sad, they can be surprising and inspiring. Each one is unique, deeply personal, and worth sharing.
Would you like to read more aha moments? Oprah.com has many aha moments from many different perspectives.
You still want more? Public Radio International has aha moments you can listen to or read.
Daniel Goleman found that nurturing the creative insight is vital. When a person offers a novel idea, instead of the next person who speaks shooting it down—which happens all too often in organizational life—the next person who speaks must be an ‘angel’s advocate,” someone who says, ‘that’s a good idea and here’s why.”
I hope this is what occurs in schools when teachers and principals have a novel idea that will help students. I know our world will improve if every teacher provides space for students to have “aha” moments. Along the way, these teachers will have aha moments, too!
Life is not measured by the number of breaths we take, but by the moments that take our breath away. —Maya Angelou
Bonus? Aha Moment Slideshow from Tabor Rotation Institute participants.
Guided Math via the Teacher Time Station
The most popular math station during a week of Tabor Rotation? In every survey, formal or informal, the answer is always Teacher Time. This is the guided math station, of the Tabor Rotation Framework, where teachers plan to teach a small group of the most difficult concepts for the week. But, what goes into a Teacher Time Station?

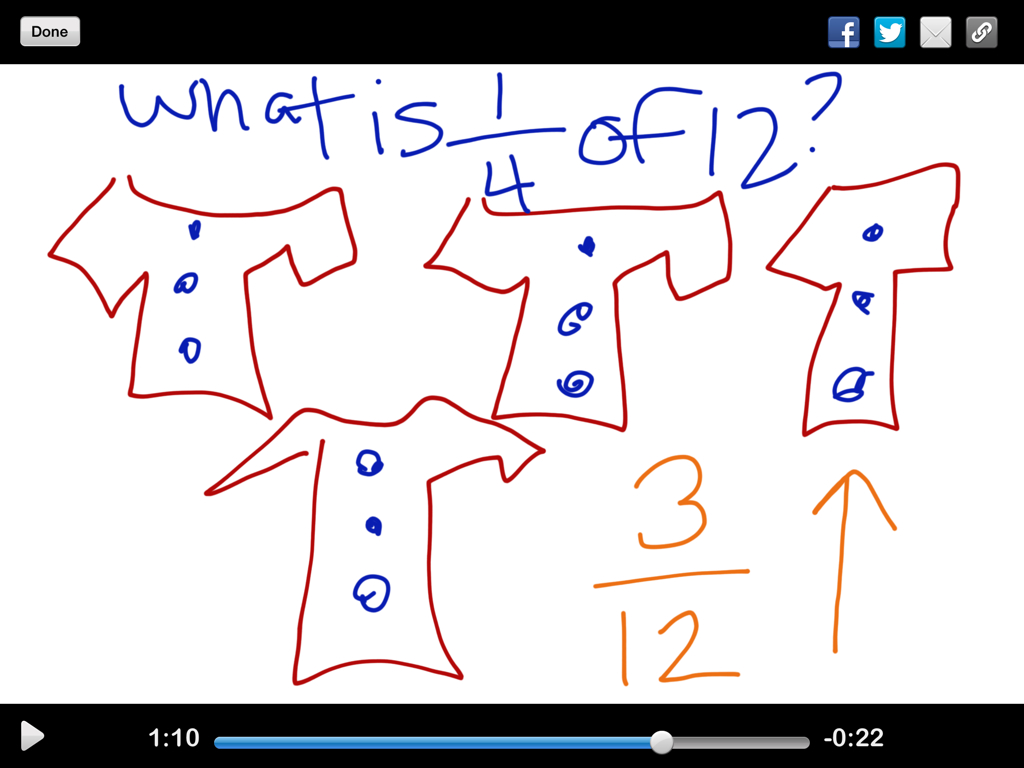
Let’s look at the contents for Teacher Time with students exploring the concept of fractional parts of a set for the first time.
Based upon a pre-assessment given four weeks before the next fraction unit began, the data indicated that none of my students knew how to determine the fractional part of a number. A few students recalled the term reciprocal, what they called “flipping it over” and thought that you had to do something with the numbers to find the fraction. But no one really understood and could explain fractional parts of a number. This information helped me develop the content for the station activities and student passports to the stations. Passports serve as an individual accountability measure and check for understanding for the stations.

The questions included in the passport are EXIT QUESTIONS and are a bridge from the hands-on activity at the math station to the way the students will be asked the question on the state test at the end of the year. This research also helped guide the type of questioning I use at the Teacher Time Station and the questions included on the formative assessment quiz.
At the bottom of each of the pages of the passport I put the REMEMBER IT! box so that students could note the most important terms or ideas from the stations.  Kind of like a one or two-word summary. (Thanks for this idea, Natalie Eppert, who began using this with her Algebra II and Geometry students a few years ago.)
Kind of like a one or two-word summary. (Thanks for this idea, Natalie Eppert, who began using this with her Algebra II and Geometry students a few years ago.)
Next, I create pair bags with manipulatives. There are enough pair bags in the station bag for each pair of students. Since my students are going to take on the real-world role of clothing designers, they will be using buttons, bling, and tiny shirts. I also give each pair of students a rectangular piece of felt to serve as their work mat. This helps define the “personal space”of each pair of students. All of these items are available from any craft or discount store. I use bandanas for the shirt fabric.

 There are several other items that are included in the Teacher Time Station Bag. The Leader Folder is always part of the Station Bag, even when I am the one guiding the instruction at the station. This way the Leader can always help facilitate the activity and the Co-Leader can ask the Exit Questions. [For more about Leader Folders and Station Bags, read the blog posts about these critical components for successful math stations.]
There are several other items that are included in the Teacher Time Station Bag. The Leader Folder is always part of the Station Bag, even when I am the one guiding the instruction at the station. This way the Leader can always help facilitate the activity and the Co-Leader can ask the Exit Questions. [For more about Leader Folders and Station Bags, read the blog posts about these critical components for successful math stations.]

I also include a white board and dry erase marker for every pair of students and one for myself. This way I can move to the abstract algorithmic procedure or steps for determining fractional parts of a number, if and when the students are ready.
My favorite components for the Teacher Time Station for exploration of fractional parts of a number have to be my “bling” apron and my metal Scotch Tape button container. The “bling” apron shows the students that they really could take the knowledge they are gaining at the station and design clothing.
My personal button container is the most powerful tool I use at the Teacher Time Station when teaching this concept, because it helps the students connect to the concept. The Scotch Tape container was given to me by my mother when I began sewing. It was given to her by her mother, so I have buttons that are almost 100 years old and each one has a piece of my history connected to it. Before the lesson begins, I ask each pair of students to pull a button and I tell the story behind the button. The students are so engaged in the lesson at this point, that finding fractional parts of a number never intimidates them. They are already hooked and connected!
But wait…there’s more…
I move these same Teacher Time Station Components to the Technology/Innovation Station the next week. Pairs of students work together to create a script for teaching other students how to find fractional parts of a number using the same manipulatives that they used. After practicing their script, the pair records the lesson using the app, Educreation. Follow this link to watch what one pair of students recorded–it’s really amazing and completes the circle of learning for the students as they use technology to innovate and create!
Why spend the time to gather buttons, pieces of bling, and cut out tiny shirts? The “aha” moments when your students truly understand fractional parts of a number will provide the answer to that question. Besides all that, it’s ENGAGING, MEANINGFUL, and FUN? Isn’t learning supposed to be exactly that?
Does Tabor Rotation work with…?
Does Tabor Rotation work with…
…CCSS-Common Core State Standards?
…TEKS-Texas Essential Knowledge & Skills?
…CCGPS-Common Core Georgia Performance Standards?
…my district’s mandated curriculum?
…the new program my district just adopted?
The list could go on and on, but the answer to every one of the questions above is YES!
Why is the answer yes? It’s simple. Tabor Rotation works with all of the above because it is an instructional framework that effectively differentiates instruction in mathematics. It’s not program–that’s the beauty of it! It’s a plan that gives teachers a way to help every student explore concepts in varied modalities and in varied groupings. The 14 Essential Elements of Tabor Rotation are good teaching practices that provide teachers and schools with a structure for best meeting the needs of every student.
Because Tabor Rotation is a framework for instruction that highlights 14 Essential Elements of effective instruction, it works at any level, with any resources, any curriculum, and any time frame!
The Tabor Rotation Framework helps teachers provide their students with many opportunities to explore, experience, practice, apply, and deeply understand math concepts.
Leslie Skinner, a 3rd grade teacher who began implementing Tabor Rotation in her classroom after a Tabor Rotation Institute in January, 2013, explains it well,
“[Tabor Rotation] is not a program, but a framework that helps teachers like me, do what I should already be doing. …All the needs of my students are met with Tabor due to the focus it places on one skill in heterogeneous and homogeneous groupings. The stations have real-world connections with lots of hands-on manipulatives and games, which helps reinforce the skill for better long-term retention. The students work in mixed ability groups to generate a more student-centered classroom by giving them the opportunity to learn from each other. The ability groups [Readiness Groups on Days 4 & 5 of the Tabor Rotation Framework] afford the students more specific instruction to help them reach their highest potential.
I strongly believe all my students passed the STAAR [State of Texas Assessment of Academic Readiness] test because of the implementation of Tabor Rotation in my classroom.”
Now for the next big question…
How can I cover all the standards, teach everything I need to teach, and use Tabor Rotation?
According to the most recent research on the skills needed in the 21st century, teachers can’t afford not to! Michael Brick, in his article, “Three Cheers for School! Building a Better School Day,” for Parade magazine, listed some “inspiring ideas to deepen learning, engage students, close achievement gaps, and better prepare our kids for a 21st-century world.”
Many of these inspiring ideas are easily accomplished if teachers use the Tabor Rotation Framework, because they’re embedded in a week of Tabor Rotation.
- Emphasize Learning, Not Testing- Our country’s emphasis on test-taking has increased pressure on teachers to “teach to the test” when students need to be able to deal well with confrontation and see two different sides to a problem [Working inTeams and completing activities at Tabor Rotation Stations, Challenges and Problem Solving in Readiness Groups and at the Teacher Time Station].
- Teach 21st-Century Skills- Students benefit in the real world when they have encountered projects that are like the real world. Long-Term Projects [Projects in the Technology/Innovation Station] teach them to persevere, revise, reflect, and hone their skills.
- Flip the Class Work- Instead of spending class time listening to the teacher lecture, students should spend class time having the concepts reinforced with interactive labs and discussions. {The entire Tabor Rotation Framework is student-centered and emphasizes students interacting with the concepts to make meaning of them and to apply them in multiple situations.]
The entire article is thought-provoking and well worth your time.
Does Tabor Rotation work?
Do I really have the time to use it?
I’ll let Charles Bucher, a secondary teacher and avid user of Tabor Rotation, answer that,
“With Tabor Rotation, I found a framework through which I was able to teach my district’s required curriculum, yet find new ways to engage and motivate students, and streamline the hurricane of paperwork and accountability required of all teachers.
With Tabor, you focus on what is important: small group and individual time with students to teach, assess, and correct. As a benefit, you get unique ideas and tools for classroom management and organization, with every element carefully tailored to the math classroom, but easily adaptable to any curriculum.
Tabor Rotation has made me the teacher I am today:
A veteran teacher ready to mentor the four new math teachers we will have next fall,
Confidently in control and calm in the classroom,
Prepared to punt in any emergency,
Organized so that data is at my fingertips and informs my teaching strategies for individual students,
Expecting more of myself and the students – we all learn every day.”
“How do we create the conditions at home, in our schools, and in our communities for students to create, learn, produce, and to innovate?” -Tony Wagner
Protected: Tabor Rotation Institute Extras
Math Stations: Big Classes Need “Pair” Bags
“Talent wins games, but teamwork and intelligence wins championships.” -Michael Jordan
That’s why teams working together at math stations are a vital component of the Tabor Rotation Framework. Effectively equipping teams for their work is imperative—especially in a math classroom at a math station!
When teachers begin to sophisticate their use of students working in math stations in a classroom, many questions arise. Here are some recently submitted after conference and institute sessions:
“How do I do this with a class of 30 students? Do I increase the team size?”
“Do you have 4 stations in large groups of students or do you implement mulitiple stations?”
“Will this work with more than 25 students? More than 30? 35?”
I created and began using the Tabor Rotation Framework when the size of my classes was close to 40 students at a time. I tried making more than four stations to accommodate more students, but I found that while I was working harder, the station rotations had to be shorter, and the in-depth understanding of concepts I wanted for my students wasn’t occurring on a regular basis.
So, I decided to make keep 4 teams–whatever the size. For an 8-member team, I divide the team into 4 pairs. The Leader helped facilitate the activity for 3 other people and the Co-Leader facilitated the activity for the remaining 3 students. Some Tabor teachers appoint two Co-Leaders when they have large team sizes.
Let’s look at an example. A class is studying geometry. On Days 2 & 3 of a week using the Tabor Rotation Framework, the Manipulative Station is set up with an activity called, “Angles and Triangles.” This activity helps students use concrete manipulatives to build a foundation for all types of angles and triangles. The activity also serves as a practice or review for students who are already familiar with most angles and triangles.
At the Manipulative Station there is a Station Bag. Inside the Station Bag are 4 Pair Bags and a Leader Folder. (10-member team = 5 Pair Bags, 12-member team = 6 bags, etc.) For more about the contents of the Station Bag and the Leader Folder, please read my last blog post, “Effective Math Stations? Leader Folders!”
For the “Angles and Triangles” Manipulative Station Activity, each Pair Bag contains:
A set of directions
A set of cards to turn over and know what to create with anglegs
A set of anglegs
A work space mat
And, an answer key
“But, does this really work?”
“YES!!!”
During the piloting phase of the Tabor Rotation Framework, multiple schools and multiple teams of teachers were asked to try 4 stations, 6 stations, and even 8 stations. The number that led to the greatest success every time was 4. The Tabor teachers who tried more than 4 stations found the same things I did. They worked harder with fewer results and less in-depth understanding from their students.
Rotating through 4 Stations, with a Heterogeneously Grouped Team, during Days 2 & 3 of a week using Tabor Rotation was the most effective grouping of students to explore concepts in varied modalities. Your classes and teams can be as large as the original Tabor Rotation ones (8-10 to a team) or as small as two. When teachers use fully-equipped Pair Bags inside fully-equipped Station Bags, everyone can focus on the mastery of math!
Download these two activities for your Manipulative Station and make as many pair bags as you need!
It Figures: Creating Congruent & Similar Figures
If you’re reading this and still asking yourself, “Why bother building math teams and creating math work stations? Maybe a thought from Mary Barnett Gilson will help,
“…there are persons who seem to have overcome obstacles and by character and perseverance to have risen to the top. But we have no record of the numbers of able persons who fall by the wayside, persons who, with enough encouragement and opportunity, might make great contributions.”
Effective Math Stations? Leader Folders!
How do I make math stations more effective?
What’s the most important resource for Leaders and Co-Leaders?
How do I make sure that students aren’t just receiving guided math instruction from me but are also guiding each other and themselves?
One answer is,
“Make sure you create a Leader Folder for every station and every activity during the Rotation to the 4 Stations [One of the 14 Essential Elements of the Tabor Rotation Framework and a vital component of a week of Tabor Rotation].”
At the end of a math conference session on Tabor Rotation last week, teachers were at the front of the ballroom looking through the sample Tabor Rotation Station Bags. As they busily studied each component of the bags, they commented on how powerful the Leader Folder must be in the success of math stations. And then, the conference center representative began “cleaning up” the station examples so the next person could prepare to present. As the rep grabbed the Leader Folders and materials from them, the teachers all looked to me for help… (at this point, I think the rep should have been afraid, but he just kept pulling all the materials)
That is why I’m blogging today about the Leader Folder and other components of a Tabor Rotation Station Bag. I asked one of the teachers to email me and ask me to write a blog on Leader Folders and she did. (I also agreed to write a blog in order to keep the conference center representative from being attacked by teachers who weren’t through studying the Leader Folders and Station Bags!)
The first item for effective math stations is a container for the station activity. Tabor Teachers have tried baskets, file boxes, crates, and colorful gift bags. The least expensive and easiest to store container for stations are the Hefty Jumbo Ziploc bags available at Target. 
Inside the station bag is the Leader Folder.

The Leader Folder has complete and thorough directions inside a clear pocket for the Leader and Co-Leader to use. There are also enough copies of the directions for each of the assigned partner pairs to study and use. Here is a sample of directions for a game for Algebra II that helps students understand, in a concrete, hands-on way, how to factor trinomials. “Tri” Factor Direction Sheet
The next clear pocket in the Leader Folder contains examples of how to complete the activity. The algorithmic procedure or steps can be shown using colored illustrations or pictures. Poly Pull Examples is an example sheet I created to help students understand how to create a polynomial using algebra tiles. Again, there needs to be enough extra copies in the side pockets of the folder for every pair of students to use.
Extra copies of work mats can be tucked into the side pockets, too. Double Ten Frame and a Place Value Chart are both examples of work mats.
There are two more items that should always be included in clear pockets inside the Leader Folder for a math work station. The state standard connected to the activity and a question, similar to the one they will be asked on the district or state test, should be included. This question will be asked by the Co-Leader as part of the Exit Questions that bridge the activity to the standard and state test.
On the back of the Leader Folder, most Tabor Teachers glue a copy of the Simple Exit Questions. Exit Questions are one of the 14 Essential Elements of the Tabor Rotation Framework and are asked at the end of every station rotation. You can download and use the standard Simple Exit Questions from the Tabor Rotation Framework to get you started.
Along with the Leader Folder, here are some other items teachers include in a Tabor Rotation Math Station Bag:
- Felt rectangles or cookie sheets to define a student’s work space and to keep manipulatives from making too much noise or rolling off a desk or table
- Bags of manipulatives– enough for each pair of students to have a bag and enough manipulatives to complete the activity without frustration
- Colorful components to grab the students’ attention and engage them in the activity
- Tiered portions of the activity to ensure that the activity is qualitatively challenging and respectful to all levels of students [Tiered Instruction is one of the 14 Essential Elements of the Tabor Rotation Framework]
“Now that I have the Tabor Rotation Station Bag and the Leader Folder prepared, how do I prepare my students to be Leaders?”
First, keep in mind that the student Leaders and Co-Leaders are not teaching the concept to their team, they are facilitating the activity, keeping their team on task, and being positive models for their team. The guided instruction for the activities at the station is planned for and occurs in the Whole-Group Mini-Lessons of a week of instruction using the Tabor Rotation Framework. [For more in-depth exploration of how to plan for and implement this type of instruction, you may want to attend a Tabor Rotation Institute.]
There are quite a few books on cultivating the leadership capacity in others. For this purpose, one of the books I read aloud to my students is John Miller’s, QBQ: Practicing Personal Accountability at Work and in Life. This book is an easy, interesting read and provides examples of the actions of true leaders. The book also illustrates how everyone can become a responsible, contributing member of any community.
Another book I provide to my students to cultivate their leadership capacity is, Shackleton’s Way, by Margot Morrell, Stephanie Capparell, and Alexandra Shackleton. Ernest Shackleton is known as one of the greatest leaders in history because of his ability to guide others, make decisions, keep the goal, and maintain morale. As so many corporate leaders and theorists have described, Shackleton was a man of great resilience and service.
Fascinated by his story and his dynamic model of leadership, I simply couldn’t put this book down. In fact, during my first reading of the book, I formed an informal book club by sharing portions with students and with participants in all of my trainings. I was making connections and just wanted to share my thoughts about his abilities and how I wanted to put those same traits into my own life.
Below are just a few excerpts about Shackleton.
“Shackleton’s first thought was for the men under him. He didn’t care if he went without a shirt on his back so long as the men he was leading had sufficient clothing.” –Lionel Greenstreet, ship’s First Officer
“Resiliency involves both the hardihood and courage to take on risks and challenges, and the ability to bounce back from difficulties and disappointments. Shackleton would face hardships that almost defy belief, and it was his iron-clad resilience that allowed he and his men to survive.
The story of the Imperial Trans-Antarctic Expedition is the story of surging optimism met with crushing defeat manifested over and over and over again. That the former never failed Shackleton, and the latter never broke him, is truly what brought his men through to the other side.” – Brett & Kay McKay, from a Man’s Life [ Read more thoughts from the McKay’s.]
This type of leadership is exactly what I want to see in all of my students, not just in math, but in every aspect of their lives. By implementing Leadership Academy, Rotation to Math Stations, and providing effective tools such as the Leader Folder and Station Bags, I am hoping to help them continue on their journey to become creators, innovators, and productive lifelong mathematicians! By writing this blog, I’m also hoping to help you on…